Recursion

Using Recursion

Lesson

You can use Recursion to solve literally every coding problem, and it's extremely useful on tree and graph problems.

Recursion is simply when you have an equation with the same function on both sides. Here are a couple examples:

f(n) = f(n-1) + f(n-2)

total(root) = root.val + total(root.left) + total(root.right)

If you can write down an equation that describes your problem like this (the same kind of equation that says 2 = 1 + 1), then you can solve it easily with Recursion. There are almost no downsides to using Recursion - in cases where it's inefficient, it can be made efficient using an extra step, either "Dynamic Programming" or "Backtracking". We'll get to these in later sections.

Here we'll solve an example problem using Recursion, and you'll learn about the 3 steps you should use to solve any problem with Recursion.

Number of Tree Nodes

Problem: Given the root node of a binary tree root, return the number of nodes in the tree.

Example:

\notag \large \texttt{=> returns 7}

First Few Test Cases:

numNodes(TreeNode.of([1]))
# 1

numNodes(TreeNode.of([1, 2]))
# 2

numNodes(TreeNode.of([1, 2, 3]))
# 3

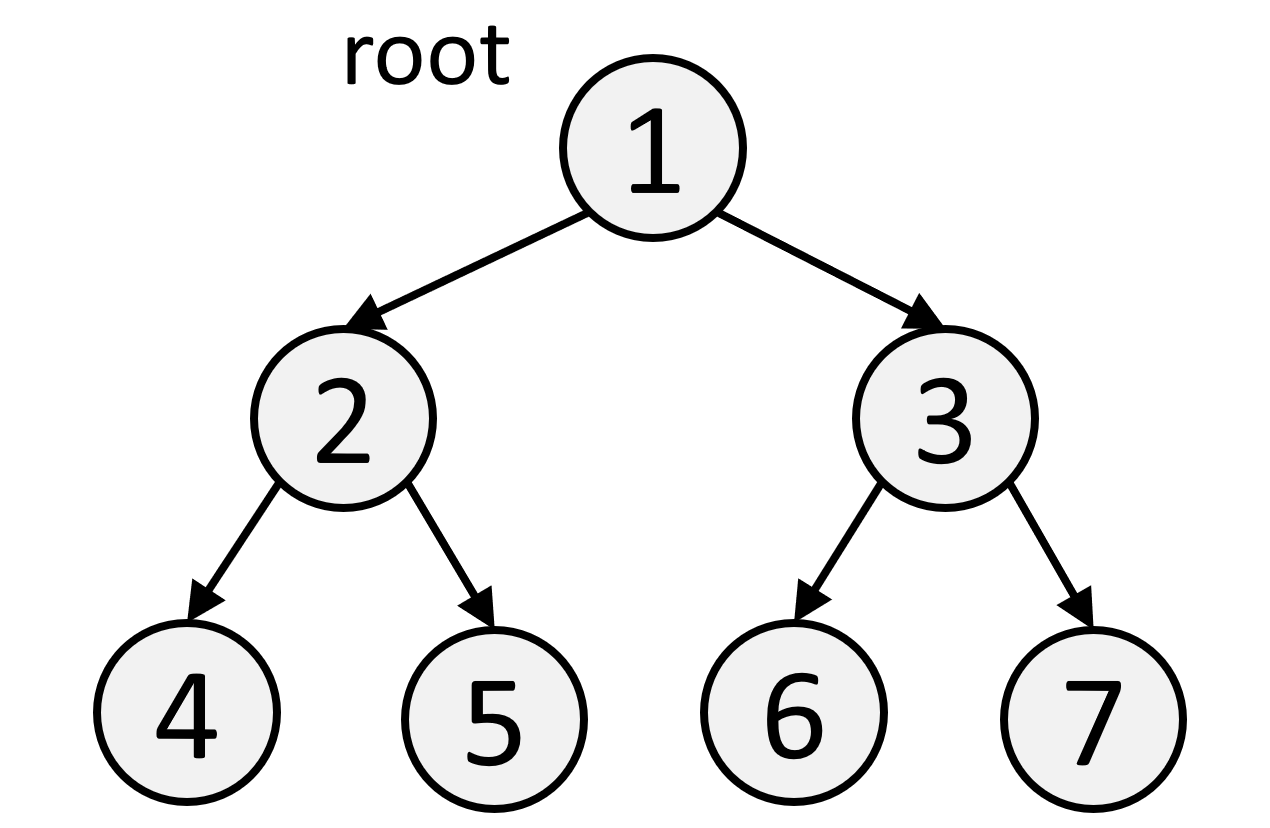
1. Recursion

Step 1 is to find a recursive equation.

In this problem, we're asked to find the the number of nodes in a tree, which we'll call numNodes(root). We want to find a Recursive equation for this, which just means we want an equation that has numNodes on both sides of it. It should look something like this:

numNodes(root) = something with numNodes(?)

How do we find this equation? In other words, what is numNodes(root) equal to?

When you're coming up with any recursion, you should think "locally" near the original problem. Here, the original problem is on the root node, so we should think about the nodes root.left and root.right. Here's a visual of this:

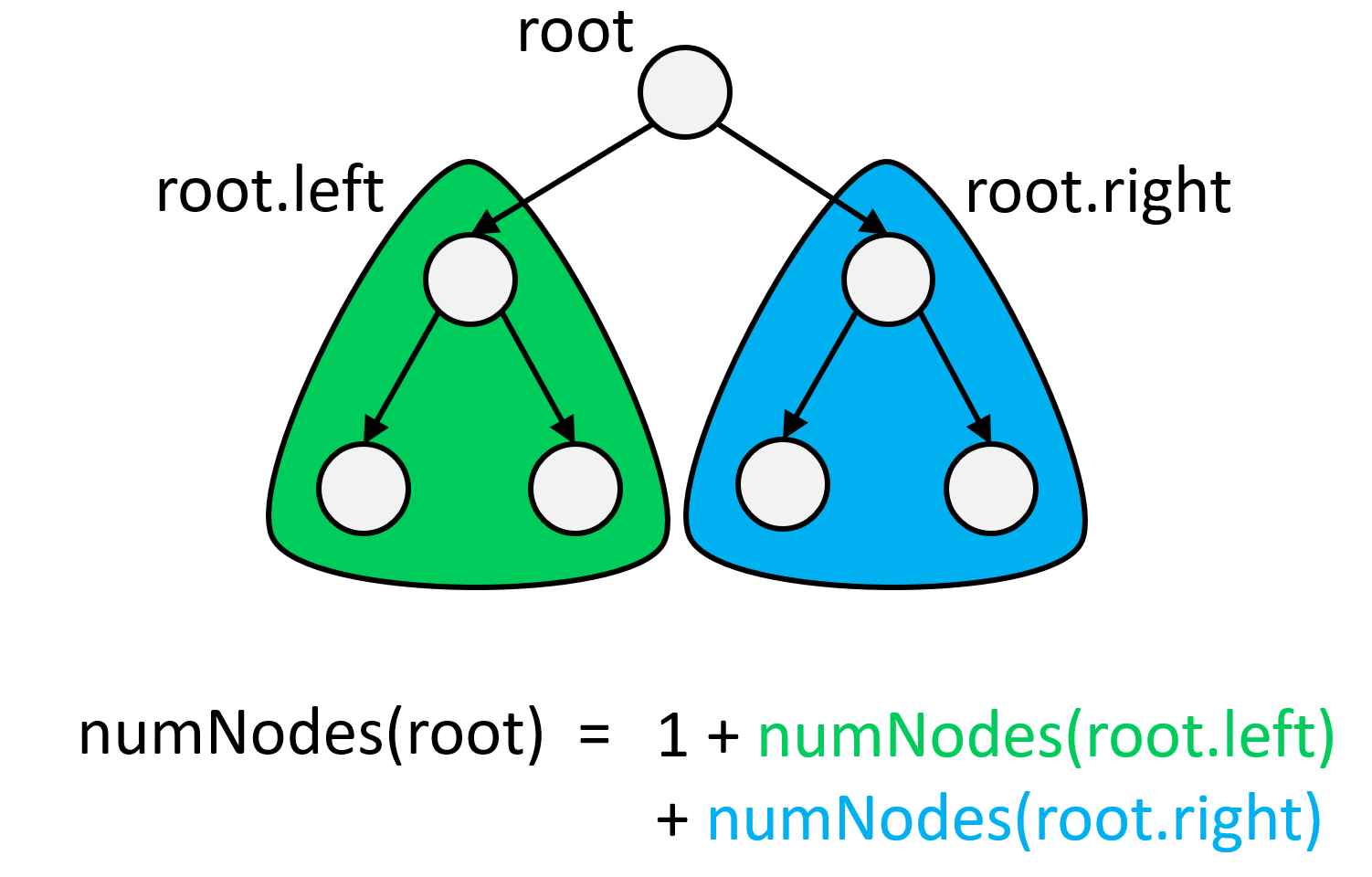
From this image, it's pretty obvious that the number of nodes in the tree is just equal to the number of nodes in the left tree, plus the number of nodes in the right tree, plus the 1 root node. This is our recursive equation - the two sides of it are equal, the same way that 1 + 1 = 2.

Typically, you should write the recursion in your code editor and discuss it with your interviewer.

2. Base case

Step 2 is to find when the recursive equation stops working. This is called the "base case".

The recursive equation here stops working if we call a null node, numNodes(None). This is because the recursion uses None.left and None.right which throws an error. We can't use the recursion to find numNodes(None), so we need to manually set what this value is equal to. The number of nodes at a null node is just 0.

numNodes(None) = 0

3. Code

Step 3 is to code up the solution.

To do this, you should write a function that always returns what numNodes is equal to. That way it's guaranteed to be correct. numNodes is always equal to the recursion, unless we're in the base case in which case it's equal to 0. Here's the full code:

def numNodes(root):
    # base case
    if root is None:
        return 0
    
    # recursion
    return 1 + numNodes(root.left) + numNodes(root.right)

Time Complexity $O(n)$ , where $n$ is the number of nodes in the tree. The recursion does roughly 1 operation on every node in the tree. This means it takes $n \cdot O(1)$ time, which is the same as $O(n)$ time.

Space Complexity $O(n)$ . For now, you don't need to know where this comes from - we'll go over the full details in the next lesson "Call Stack". Just know the computer needs some memory to keep track of the function calls it's making.

Mark as Completed:

Submits:

numNodes

Imports:

TreeNode

Test your code to get an output here!

numNodes(

)

Test your code to get an output here!